



Next: Algorithm and implementation
Up: Surface Triangulation
Previous: Surface Triangulation
The input for the surface triangulation routine implemented here is
the bilinear Coons surface/patch [GH73,RA90].
If the four boundary curves in (u,v) space, P(u,0), P(u,1),
P(0,v) and P(1,v) are known, and a bilinear blending function is used
for the interior of the surface patch, a linear Coons surface is obtained.
It is given by
where 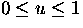 ,
, 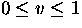 .
It can be easily seen that, at the corners,
.
It can be easily seen that, at the corners,
P'(0,0) = P(0,0), P'(0,1)=P(0,1), P'(1,1)=P(1,1), P'(1,0)=P(1,0)
and along the boundaries,
P'(u,0) = P(u,0), P'(u,1)=P(u,1), P'(0,v)=P(0,v), P'(1,v)=P(1,v)
More compactly, the equation can written as
![\begin{displaymath}
P'(u,v) =
\left [ \begin{array}
{ccc} 1-u & u & 1 \\ \end{...
...ft [ \begin{array}
{c} 1-v \\ v \\ 1 \\ \end{array} \right ]\end{displaymath}](img32.gif)
A mapping function then gives (x,y,z) corresponding to every (u,v).
In the implementation here, the four boundary curves happen to be B-spline
curves (BSCs). The functions (1-u), u, (1-v), and v are called
blending functions because they blend the boundary curves to produce the
internal shape of the surface.
The linear Coons surface is the simplest of the Coons surfaces. Examples
of these surfaces are Figures 6.1 and 6.2. A
C code for IITZeus using X/Motif was written as a part of this project to
obtain this.
Figure 6.1:
Linear Coons surface (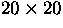 )
)
 |
Figure 6.2:
Linear Coons surface (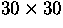 )
)
 |




Next: Algorithm and implementation
Up: Surface Triangulation
Previous: Surface Triangulation
Anirudh Modi
1/16/1998
![]() ,
, ![]() .
It can be easily seen that, at the corners,
.
It can be easily seen that, at the corners,
![\begin{displaymath}
P'(u,v) =
\left [ \begin{array}
{ccc} 1-u & u & 1 \\ \end{...
...ft [ \begin{array}
{c} 1-v \\ v \\ 1 \\ \end{array} \right ]\end{displaymath}](img32.gif)