Algorithm and implementation

1.

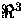Four BSCs with C⁰ continuity (end-points being common) are read from the database, and a Coons Surface is made from it, i.e., a one-to-one mapping function from (u,v)-space $([0,1] \times [0,1])$ to (x,y,z)-space ($\Re^3$) is established.

2.

The 2D (u,v)-space is now triangulated using graded triangulation described earlier. Here, the major change is the use of the actual 3D lengths of the segments as one of the additional grading parameters. This means that whenever a trial point in (u,v)-space is chosen, the corresponding point in 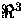$\Re^3$ is determined and its 3D distances with the neighbouring points in the front is also used to re-adjust the original point. This is done by simple iteration till some kind of convergence is obtained between the two consecutive points.

3.

Thus, the triangulation takes place in pseudo-3D and whenever a point in (u,v)-space is inserted, it is mapped back to 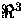$\Re^3$and the corresponding triangle is displayed.