Voronoi tessellation

Before attempting to learn about Delaunay triangulation it is helpful to learn about Voronoi tessellation also known as Theissen or Dirichlet [Bow81] tessellation. Voronoi tessellation is a geometric dual of Delaunay triangulation and one can be derived from the other. Given a set of N points in a plane, Voronoi tessellation divides the domain in a set of polygonal regions, the boundaries of which are the perpendicular bisectors of the lines joining the points (Figure 4.1).

  

Figure 4.1: Voronoi tessellation and Delaunay triangulation

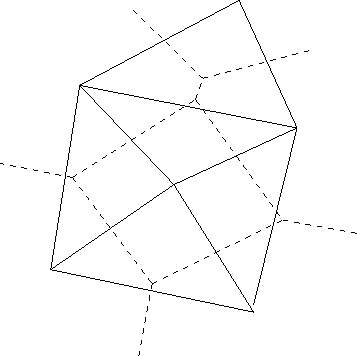Furthermore each tile contains only one of the N points. If both these conditions are satisfied then the lines joining the points form a mesh known as the Delaunay triangulation. According to the Delaunay criterion, the circumcircle of every triangle is so formed that it does not contain any point of the mesh. Except in degenerate cases, the vertices of Voronoi tessellation occur where three tiles meet. Each Voronoi vertex is circumcenter of a Delaunay triangle. In degenerate cases more than one triangle may be validly possible.

Since Delaunay triangulation is the geometric dual of Voronoi tessellation, many methods have been formulated to arrive at the former using the latter, though many methods for direct triangulation have also been formulated [HS88,LS80]. In Delaunay triangulation the boundary triangulation is not difficult but placing the interior points at inappropriate places may result in bad meshes even though the Delaunay criterion is satisfied.