Conformity

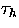The set $\tau_h$ is a conformal mesh of domain 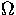$\Omega$(Figure 2.1), iff

1.

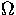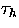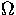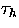The domain $\Omega$ is completely and exactly covered by the mesh $\tau_h$. When the domain $\Omega$ is not polygonal (in 2D) or polyhedral (in 3D) (i.e., if it is defined by a smooth curve or a surface), the mesh $\tau_h$ will only be an approximate partitioning of the domain.

2.

All elements of mesh 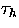$\tau_h$ must have a non-empty interior.

3.

The intersection of any 2 elements in the mesh 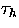$\tau_h$ is either an empty set, a point, an edge or a face (of both elements).

  

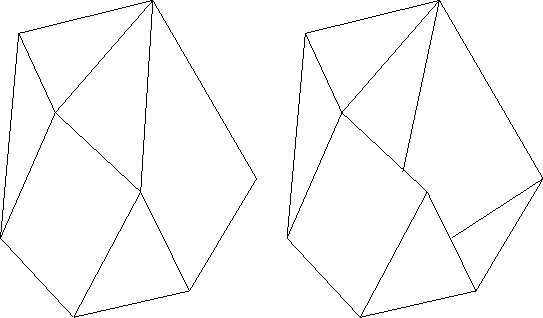
Figure 2.1: Conformal and non-conformal meshes