



Next: Efficiency
Up: Graded Triangulation
Previous: Algorithm
The above algorithm requires the implementation of both the Delaunay
triangulation and the AFM. These have been done as described in the previous
chapters. The algorithm can now be described as -
- The domain/boundary is read (only one level of holes
are allowed for need of continuum) and
converted to a PLC if not already so.
- Initial Delaunay triangulation is done using these boundary
points and the triangles are stored in a TRI
structure [Nan95].
- The node density of each boundary point is now computed using
the above information and stored. This is simply the
mean of all the edges in the triangulation meeting at that
point.
- Now, the AFM proceeds and the function for determining the
new insertion point is modified as follows -
- 1.
- A first approximation to the insertion
point (called trial point) is made in the same way as
described earlier for the conventional AFM.
- 2.
- Using this point,
the background triangle containing the point
is found using a simple search algorithm.
- 3.
- Upon finding this background triangle, the
barycentric coordinates (
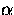 ,
, 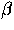 and
and
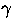 ) of the trial point w.r.t. the triangle is
computed. These are simply the ratios of the area of the
three triangles formed by the trial point and the
background triangle to the area of the background
triangle.
) of the trial point w.r.t. the triangle is
computed. These are simply the ratios of the area of the
three triangles formed by the trial point and the
background triangle to the area of the background
triangle.
- 4.
- The already computed node densities of the nodes
of the background triangle (L1, L2 and L3)
are now recalled.
- 5.
- The new length of the trial point from the edge
of the front is now recomputed based on a suitable
function of the above 6 parameters
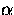 ,
, 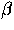 ,
, 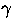 , L1, L2 and L3.
, L1, L2 and L3.
- 6.
- Having got a new trial point, iteration
starts again from 2, till the next
point obtained
by the procedure is the same as the previous point or
within a certain tolerance band of the previous point.
- Having got the final insertion point, the AFM proceeds
till the triangulation is completed.
Also, apart from the above mentioned 6 parameters, the gradation function
is implemented to accept two additional parameters x and y which
specify the location of the current trial point.




Next: Efficiency
Up: Graded Triangulation
Previous: Algorithm
Anirudh Modi
1/16/1998
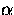 ,
, 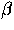 and
and
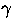 ) of the trial point w.r.t. the triangle is
computed. These are simply the ratios of the area of the
three triangles formed by the trial point and the
background triangle to the area of the background
triangle.
) of the trial point w.r.t. the triangle is
computed. These are simply the ratios of the area of the
three triangles formed by the trial point and the
background triangle to the area of the background
triangle.
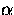 ,
, 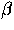 ,
, 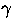 , L1, L2 and L3.
, L1, L2 and L3.