



Next: Implementation
Up: Graded Triangulation
Previous: Introduction
A popular method of graded triangulation is by use of a background mesh
for the entire domain. The background mesh is a triangulated mesh generated
using only the boundary points. Such a mesh can be generated by the use
of initial Delaunay triangulation. Now the graded triangulation differs
from the AFM only in that
the function for calculating the trial point is modified to
accommodate the grading. This function now uses the information of the
background mesh such that the length of the triangle's edges increase from
the minimum value to the maximum. At any point in the domain the edge
length of the sides of the triangle under construction are calculated to
ensure gradual variation by finding the background triangle that encloses
the point. The barycentric coordinates of the point with respect to the
three nodes of the triangle are calculated. The mesh density at any
node is defined as the mean of the lengths of the edges meeting at that
point. If the mesh density at the nodes of the triangle containing the
point are L1, L2 and L3 and the respective
barycentric coordinates of the
point are 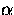 ,
, 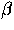 and
and 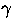 (note that
(note that
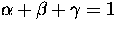 ), then the required lengths of
the new edges are given by
), then the required lengths of
the new edges are given by
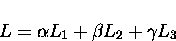
The disadvantage of this method is that the Delaunay triangulation for
initial triangulation should be done before starting the actual
triangulation, but it results in a far better mesh than direct
graded triangulation which does not use any background mesh.




Next: Implementation
Up: Graded Triangulation
Previous: Introduction
Anirudh Modi
1/16/1998
![]()